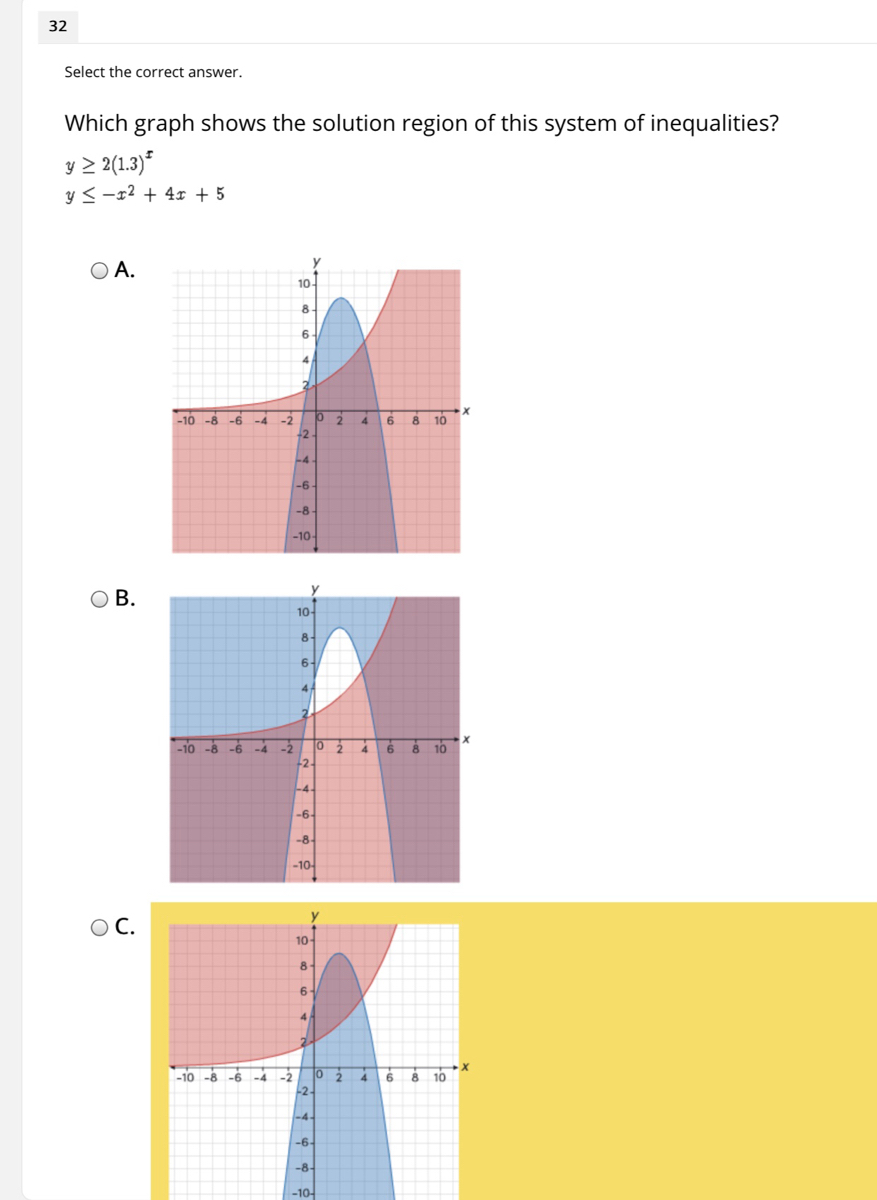
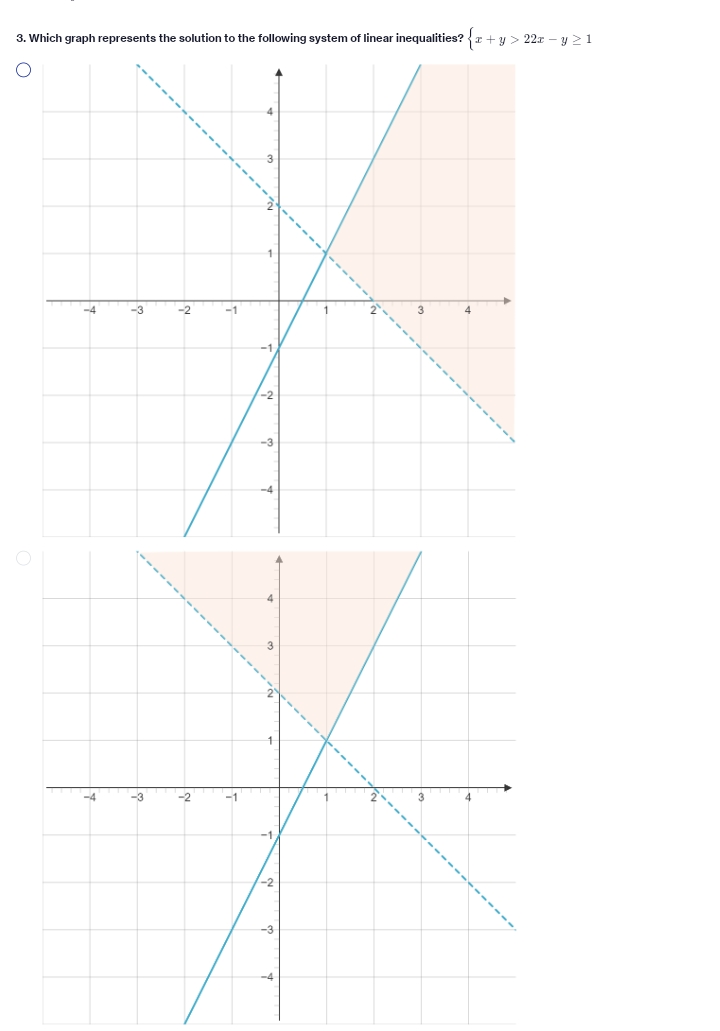
Which Graph Shows The Solution To This System Of Inequalities
Which Graph Shows The Solution To This System Of Inequalities Brainly Com
Which graph shows the solution to this system of inequalities. When we take both of the linear inequalities pictured above and graph them on same Cartesian plane we get a system of linear inequalities. The fourth graph will be the solution. There are endless solutions for inequalities.
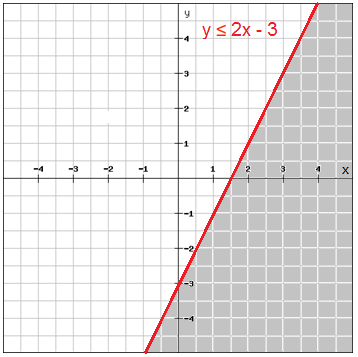
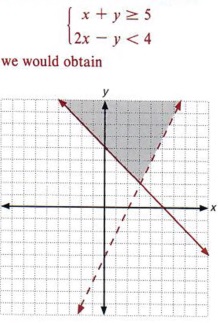
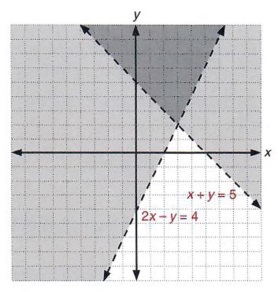
Inequalities that uses either the or sign are plotted using a dashed line while inequalities with makes use of or are plotted using the solid line. To graph the solution to this system we graph each linear inequality on the same set of coordinate axes and indicate the intersection of the two solution sets. Solutions to a system of linear inequalities are the ordered pairs that solve all the inequalities in the system.
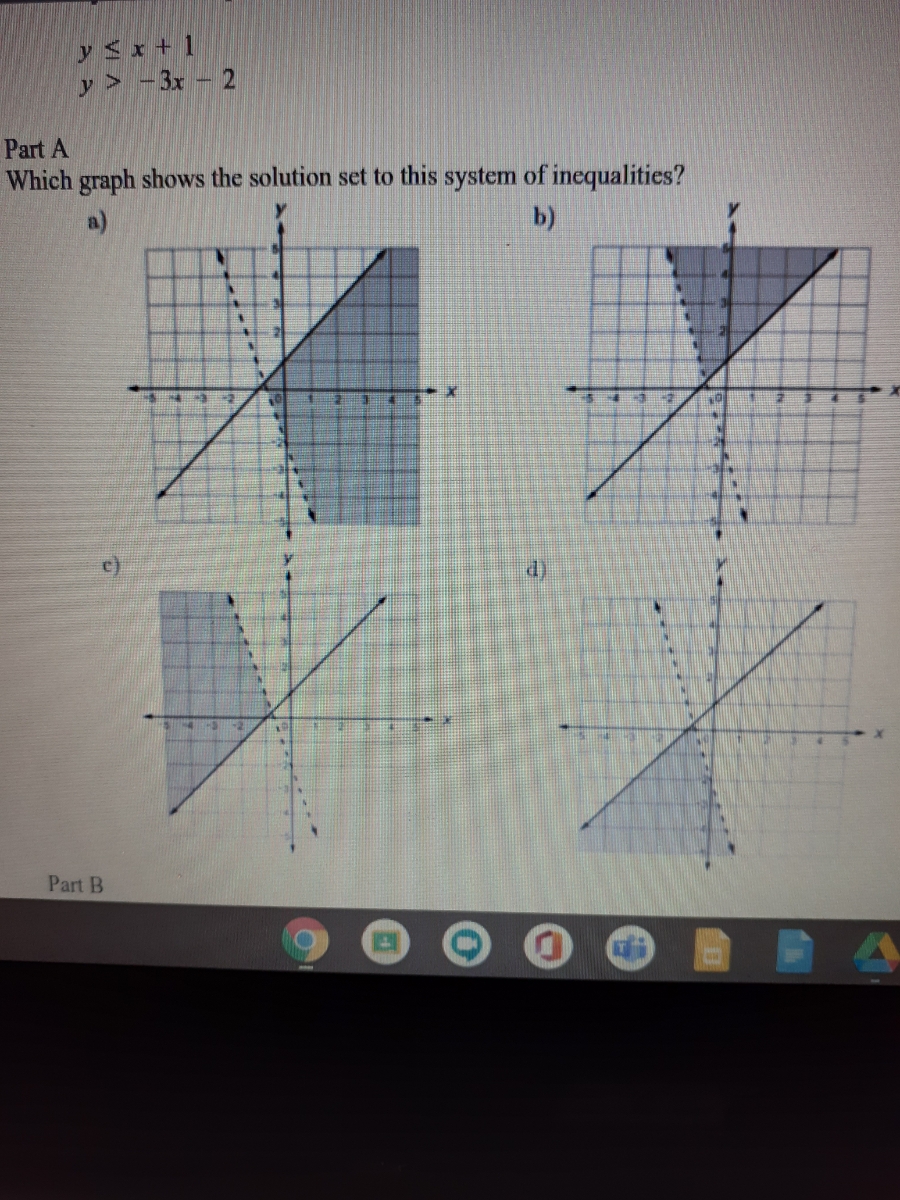
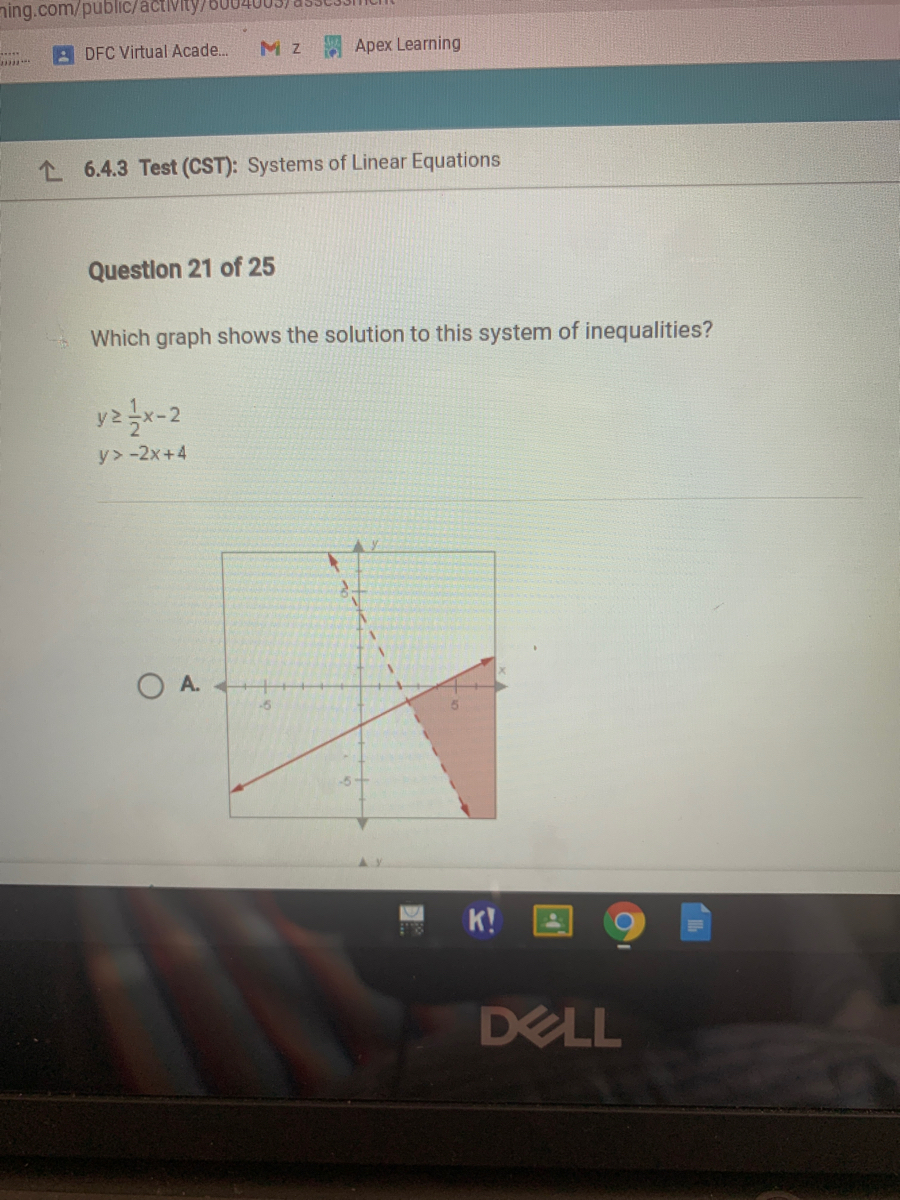
How To Solve Systems of Inequalities Graphically. Mathematics 27102020 0210 rockstargirl9869 Which graph shows the solution to the system of inequalities below xY. Therefore to solve these systems graph the solution sets of the inequalities on the same set of axes and determine where they intersect.
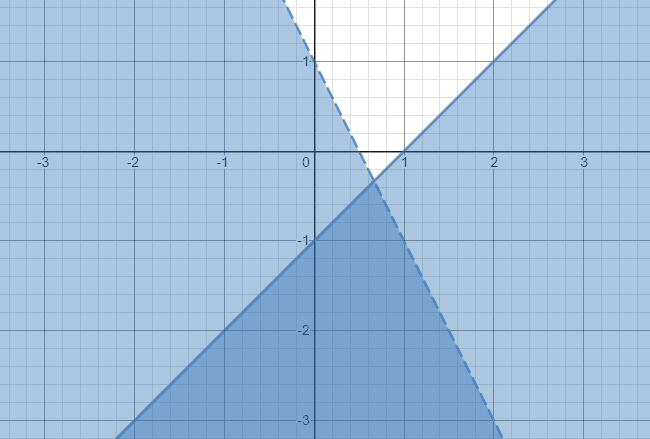
To graph a linear inequality in two variables say x and y first get y alone on one side. Example number two may have looked confusing at first because of the inequalities. The solution to a system of inequalities in two variables is often shown as a shaded graph on the coordinate plane.
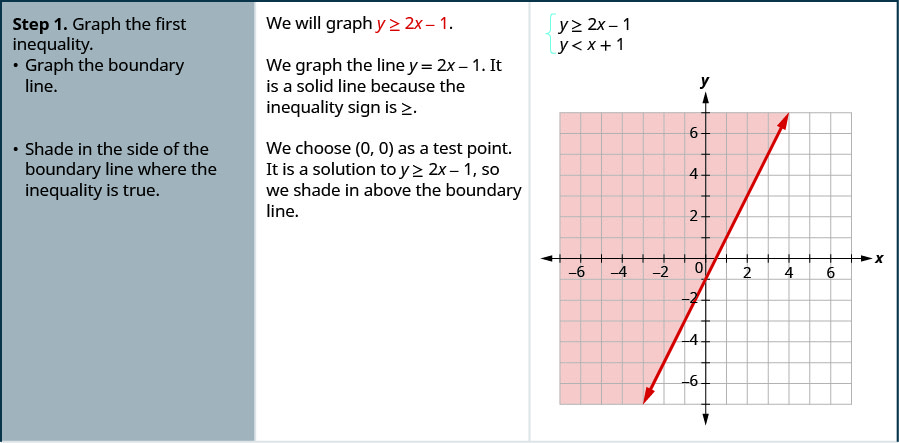
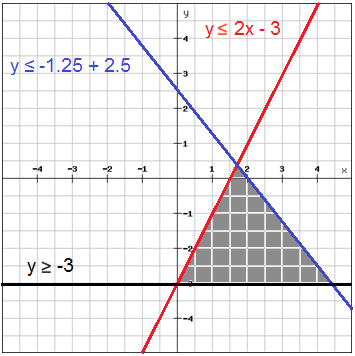
A solution of a system of linear inequalities is an ordered pair that is a solution of each inequality in the system. Click card to see definition. KEY CONCEPT For Your Notebook Graphing a System of Linear Inequalities STEP 1 Graph each inequality.
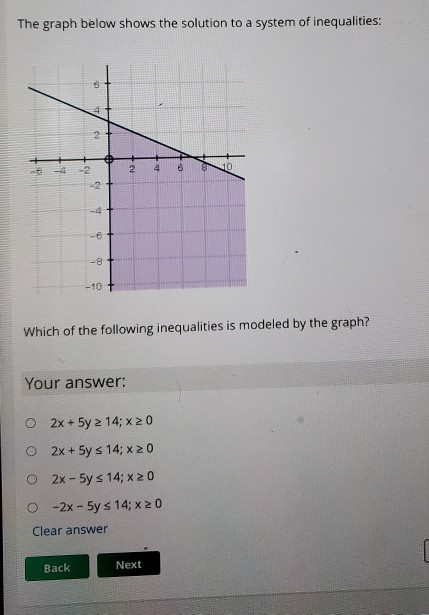
The graph that shows the solution is A. Solving Systems of Linear Inequalities. Y 13x 3 and 3x - y 2 Which graph shows the solution to the system of linear inequalities.
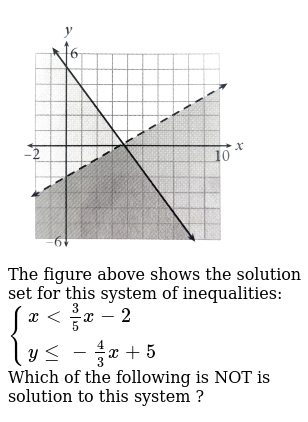
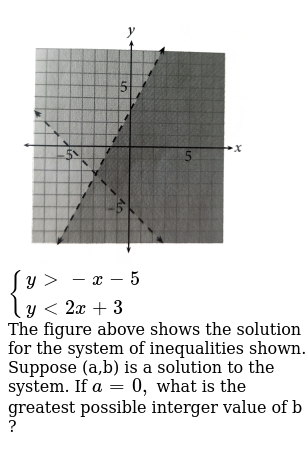
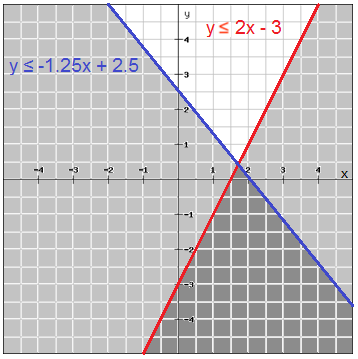
The system of linear inequalities are - 3x - 3y - 3 x y 1 And y -x 1 x y 1 There is no solution for those two inequalities because there are no values of x and y that can satisfy both the equations. Then consider the related equation obtained by changing the inequality sign to an equality sign.
Which Graph Shows The Solution To This System Of Inequalities Y Gt 2x 3 Brainly Com
Which Graph Shows The Solution To This System Of Inequalities Y Lt 1 2 X 2 Y 2x 4 Brainly Com
Please Help Which Graph Shows The Solution To This System Of Inequalities Brainly Com
Solved 1 Point Which Graph Shows The Solution To The System Chegg Com
Solved Which Graph Shows The Solution To This System Of Chegg Com
Best Answer Which Graph Shows The Solution To This System Of Inequalities X Y Gt 4 X Y Lt 3 Brainly Com
Solved Question 19 Of 29 1 Point Which Graph Shows The Chegg Com
Solved Which Graph Shows The Solution To The System Of Chegg Com
Which Graph Shows The Solution To The System Of Linear Inequalities Y 2x 5 Y Gt 3x 1 Brainly Com
Which Graph Shows The Solution To The System Of Linear Inequalities Below Brainly Com
Answered Select The Correct Answer Which Graph Bartleby
Answered Use The System Of Inequalities To Bartleby
Which Graphs Represents The Solution Set Of The System Of Inequalities Quora
Which Graph Shows The Solution To The System Of Linear Inequaliti
Which Graph Shows The Solution To This System Of Inequalities X 3
Answered 3 Which Graph Represents The Solution Bartleby
View Question Which Graph Represents The Solution Set To The System Of Inequalities
Solved The Graph Below Shows The Solution To Which System Of Chegg Com
Which Graph Represents The Solution Set To The System Of Inequalities Y 14x 2y 54x 2
This Graph Shows The Solutions To The Inequalities Does The System Of Inequalities Y Gt 3x 14 And Brainly Com
Solved The Graph Below Shows The Solution To A System Of Chegg Com
Systems Practice Pdf Inequality Mathematics Equations
The Graph Shows The Solution To Which System Of Inequalities
The Graph
Oneclass Which Graph Shows The Solution To The System Of Linear Inequalities X 4y Lt 4 Y Lt X
Solved Which Graph Shows The Solution To The System Of Linear Inequalities Below Course Hero
4 2 Graphing Systems Of Linear Inequalities Mathematics Libretexts
Which Graph Represents The Solution Set Of The System On Inequalities Y 2x 2 Y X 4 Hurrryy Pleaseeeeee Im Testing Studydaddy Com
Which Graph Best Represents The System Of Linear Equations And The Solution Youtube
Graphing Systems Of Inequalities
Systems Of Linear Inequalities Algebra 1 Systems Of Linear Equations And Inequalities Mathplanet
Graphing Systems Of Inequalities
Which Graph Shows The Solution To The System Of Linear Inequalities Y Ys 3x 2
Systems Of Linear Inequalities Algebra 1 Systems Of Linear Equations And Inequalities Mathplanet
Systems Of Linear Inequalities Algebra 1 Systems Of Linear Equations And Inequalities Mathplanet
System Of Linear Inequalities Explanation Examples
Graph Graph Inequalities With Step By Step Math Problem Solver
Answered Questlon 21 Of 25 Which Graph Shows The Bartleby
2
Graphing And Solving Linear Inequalities Ck 12 Foundation
Graphing Systems Of Inequalities
Consider This System Of Inequalities X Y 3 Y Gauthmath
4 7 Graphs Of Linear Inequalities Mathematics Libretexts
Graphs And Solutions To Systems Of Linear Equations Beginning Algebra
Graph Graph Inequalities With Step By Step Math Problem Solver
Solved Which Graph Shows The Solution To The System Of Linear Inequalities Below Course Hero
Systems Of Inequalities Graphing Quiz Quizizz
Find The Linear Inequalities For Which The Shaded Region In The Given Figure Is The Solution Set Youtube
Which Graph Shows The Solution To The System Of
For example 625 is a solution of the system above.
Note that the solution to a system of linear inequalities will be a collection of points. This intersection or overlap defines the region of. Example number two may have looked confusing at first because of the inequalities. When we take both of the linear inequalities pictured above and graph them on same Cartesian plane we get a system of linear inequalities. Solving Systems of Linear Inequalities. The graph of a system of linear inequalities is the graph of all solutions of the system. A vertical line is always graphed when the equation or inequality begins with x a constant. A system of linear inequalities in two variables consists of at least two linear inequalities in the same variables. KEY CONCEPT For Your Notebook Graphing a System of Linear Inequalities STEP 1 Graph each inequality.
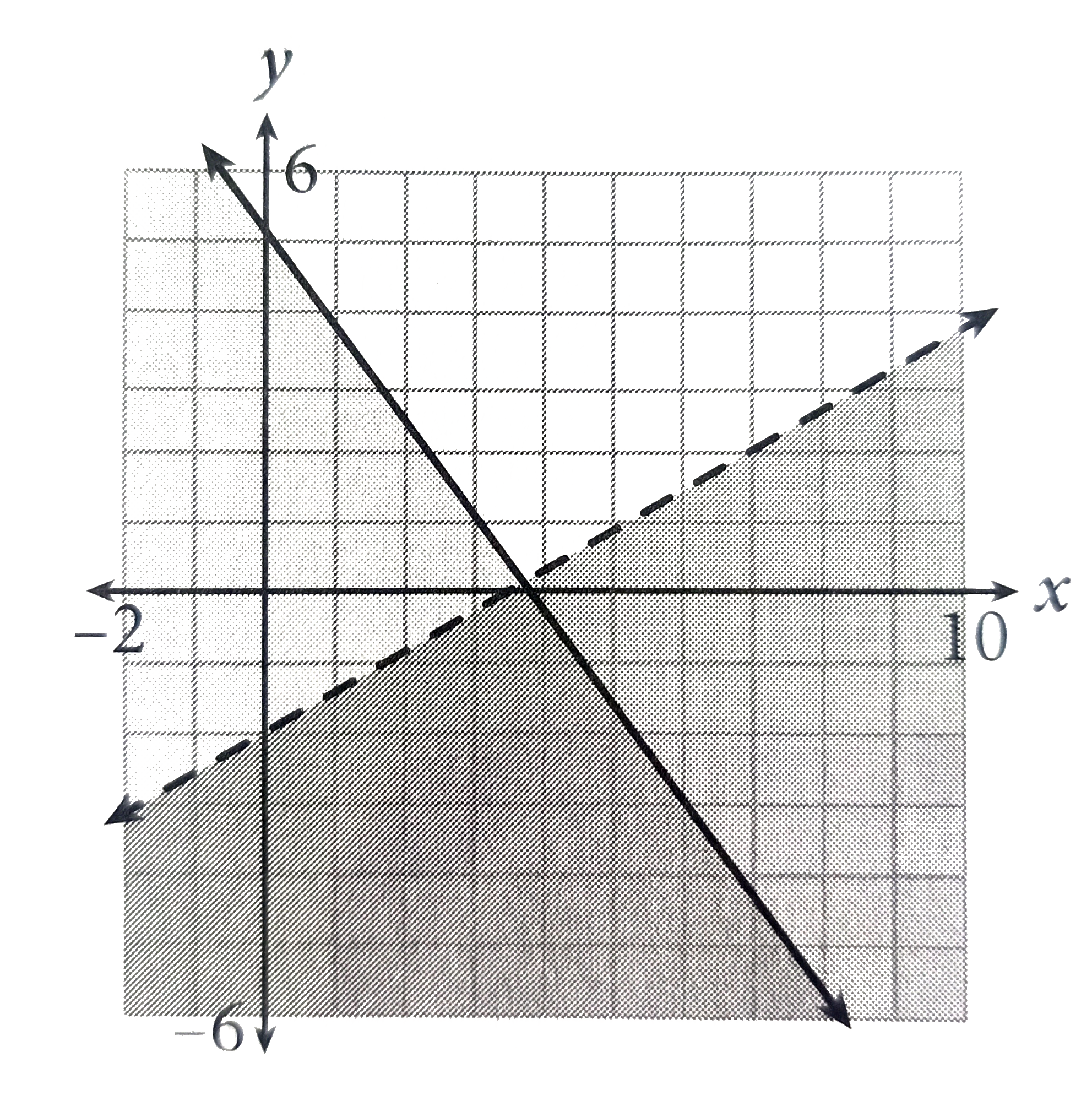
Answer to The following graph shows the solution to which system of inequalities. To solve a system of inequalities graph each linear inequality in the system on the same x-y axis by following the steps below. The solution of this system is the yellow region which is the area of overlap. This intersection or overlap defines the region of. If the inequality is strict or graph a dashed line. Tap card to see definition. Which graph shows the solution to this system of inequalities.
Post a Comment for "Which Graph Shows The Solution To This System Of Inequalities"